ABOUT APPLICATION OF INTELLECTUAL NEURO-FUZZY SYSTEMS IN ELECTRONIC BUSINESS
Lesia Nesteruk and Tatiana Nesteruk St. Petersburg State University Of Economic And Finance, Russia

The usage area of intellectual systems consists from a number of actively developing branches of internet technologies, such as electronic business, electronic commerce and electronic marketing. The fundamental purpose of similar systems application is extract knowledge from large sizes of source information (data mining and knowledge engineering). Data mining is the extraction of knowledge from data. It can also be defined as the exploration and analysis of large quantities of data in order to discover meaningful patterns and rules.

Each intelligent component has its own strengths and weaknesses. Tab. 1 [1] presents a comparison of different intelligent technologies. They are: expert systems (ES), fuzzy systems (FS), artificial neural networks (ANN) and genetic algorithms (GA). Probabilistic reasoning is mainly concerned with uncertainty, fuzzy logic with imprecision, neural networks with learning, and evolutionary computation with optimization.

Table 1

The terms used for grading are:  à - bad, ¨ - rather bad, o - rather good, � - good.

A good hybrid system brings the advantages of these technologies together. Their synergy allows a hybrid system to accommodate common sense, extract knowledge from raw data, use human-like reasoning mechanisms, deal with uncertainty and impreci�sion, and learn to adapt to a rapidly changing and unknown environment.

Artificial neural networks and fuzzy logic are complementary tools in build�ing intelligent systems. Integrated neuro-fuzzy systems can combine the parallel computation and learning abilities of neural networks with the human�like knowledge representation and explanation abilities of fuzzy systems.

Neuro-fuzzy systems. The junction of technologies of neural networks and fuzzy logic is the most perspective approach to organization of systems of an artificial intelligence for the purposes of electronic business. The systems of fuzzy logic cancel two fundamental disadvantages of neural networks, namely: in knowledge representation and explanation ability of an intellectual system. The fuzzy logic allows to formalize the qualitative information obtained from the experts in the given field of knowledge, and to present the qualitative information as a system of indistinct predicate rules.

The neural networks enable to map algorithms of the indistinct inference in structure of neural networks. The similar mapping enters in an information field of a neural network the prior information obtained from the experts in a concrete area of knowledge. The neuro-indistinct system represents a neural network, which is an adaptive functional equivalent of indistinct model of a lead-out, for example, Mamdani algorithm [2].

Although neural networks are used for solving a variety of problems, they still have some limitations. One of the most common is associated with neural network training. The back-propagation learning algorithm that is often used because it is flexible and mathematically tractable has a serious drawback: it cannot guarantee an optimal solution.

The decision of the mathematical task of multiparameter optimization of fitness function  is necessary. It is necessary to find a global maximum for fitness function.

Evolutionary neuro-fuzzy networks. Genetic algorithms (GA) are an effective optimization technique that can guide both weight optimization and topology selection [3]. To use genetic algorithms, we first need to represent the problem domain as a chromosome. Suppose, for example, we want to find an optimal set of weights for the multilayer feedforward neural network shown in fig.1.

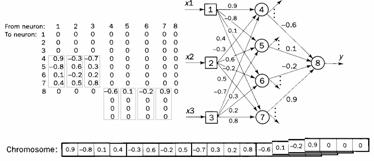
Fig.1

The set of weights can be represented by a square matrix in which a real number corresponds to the weighted link from one neuron to another, and 0 means that there is no connection between two given neurons. In total, there are 16 weighted links between neurons in fig.1. Since a chromosome is a collection of genes, a set of weights can be represented by a 16-gene chromosome, where each gene corresponds to a single weighted link in the network. Thus, if we string the columns of the matrix together we obtain a chromosome.

The next step is to define a fitness function for evaluating the chromo�some's performance. This function must estimate the performance of a given neural network. We can apply here a fairly simple function defined by the reciprocal of the sum of squared errors. To evaluate the fitness of a given chromosome, each weight contained in the chromosome is assigned to the respective link in the network. The training set of examples is then presented to the network, and the sum of squared errors is calculated. The smaller the sum, the fitter the chromosome. In other words, the genetic algorithm attempts to find a set of weights that minimizes the sum of squared errors.

Representation of an information field of a ANN as a system of fuzzy links allows to alter processes of evolutional tutoring of neuro-fuzzy systems. The fuzzy link in an information field of ANN structure with point-to-point communications features a system of interneuron links between an exit of a concrete formal neuron of a concrete layer of a network and appropriate inlets of formal neuron of a following layer of ANN [2]. If the local link (in a system of fuzzy link ) is a gene, the fuzzy link is chromosome. 

Genes by separate chromosome are values of weights of weights of links bound with exits of appropriate formal neurons, instead of with inlets, as in [3]. Chromosome is a group of weights located in a separate column of a matrix of weights of ANN (fig. 1).

The third step is to choose the genetic operators - inversion and mutation. A inversion operator changes the order of a disposition of genes in chromosomes, for example, by cyclical permutation (random amount of time) and creates a single child with genetic material from parent.

A mutation operator randomly selects a gene in a chromosome and adds a small random value between 0 and 1 to each weight in this gene.

The fuzzy  link is described to  the semantic data, which is equivalent of fuzzy set of the membership function. The fuzzy link is described by a tuple á1, s, dñ, where 1 - true value (core) of the semantic data, s - type of semantics, d - grain size of representation of semantics. Number of points of the membership function is  and each point are correspondence, both concrete real value of an fuzzy set, and particular number (fig. 2). The separate genes and chromosome can be presented by a sequence of numbers of points of semantics. With separate numbers of points of semantics evolutionary algorithms also will operate.

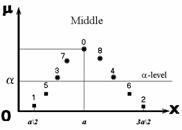
Fig. 2

Chromosome  consists of a constant gang of genes (for given grain size of semantics). Values of genes are the degrees of a truth from of a fuzzy set of the membership function.  If during realization of algorithm of tutoring of a ANN the grain size of semantics d varies, the number of genes in a gang varies as . The process of evolution is bound with permutation of genes in fuzzy link (operator of inversion). The magnification of the parameter d allows more precisely to fulfil a condition of the fitness function.

It is expedient to combine computational methods and optimizations in the comprehensive approach for a drop of expenditures of time:

- To use not pseudo-random generation of parameters at forming the initial population of a series of neural networks , and, vice-versa, beforehand to conduct tutoring each of a neural network with different initial values of parameters by means of algorithm with the abbreviated number of cycles of tutoring and on a restricted training sample.

- In case of neuro-fuzzy networks the similar outcomes of preliminary tutoring can be obtained by means of writing in frame of an ANN of different variants of fuzzy predicate rules formed by a series of the experts.

- To use multiagent of a process engineering for tutoring neural networks by means of parallel tutoring of  ANN.

- To select variants of ANN from a population by means of evolutionary methods with values of parameters near to a global optimum of the solved task/

- To produce further optimization for select variants of a neural network by methods of a gradient descent.

Inference about expediency of usage of different intellectual process engineerings for problem solving of electron business whence follows. Integrated neuro-fuzzy systems can combine the parallel computation and learning abilities of neural networks with the human�like knowledge representation and explanation abilities of fuzzy systems

References

Negneyitsky M. Artificial intelligence: a guide to intelligent systems. Addison-Wesley, 2002.

Kruglov V.V., Borisov V.V. Artificial neural networks. The theory and practice // 2-d ed. - Moscow: Hotline - Telecom, 2002.

Montana D.J., Davis, L. Training feedforward networks using genetic algorithms,  Proceedings of the  11th International Joint Conference on Artificial Intelligence, Morgan Kaufmann, San Mateo, CA, 1989. P. 762-767.